ScrewSplat:
An End-to-End Method for Articulated Object Recognition

Screw theory provides a natural mathematical formulation for describing screw motion, which involves a rotation about an axis combined with a translation along that same axis.

Recently, 3D Gaussian Splatting has been developed for novel-view synthesis from multiple RGB images and can also be used to obtain a 3D representation of scenes. Its core idea is to initially randomly splat 3D textured Gaussians and then optimize their poses, sizes, and color textures to represent the scene -- i.e., by minimizing an RGB rendering loss function.

The key intuition behind ScrewSplat originated from the question: Could we design an effective method that, similar to 3D Gaussian Splatting, ``splats''' screws to discover the kinematic structures of articulated objects? Our approach begins by randomly initializing screw axes alongside 3D Gaussians, which are then jointly optimized to recover the object’s part-aware geometry and kinematic structure in an end-to-end manner.

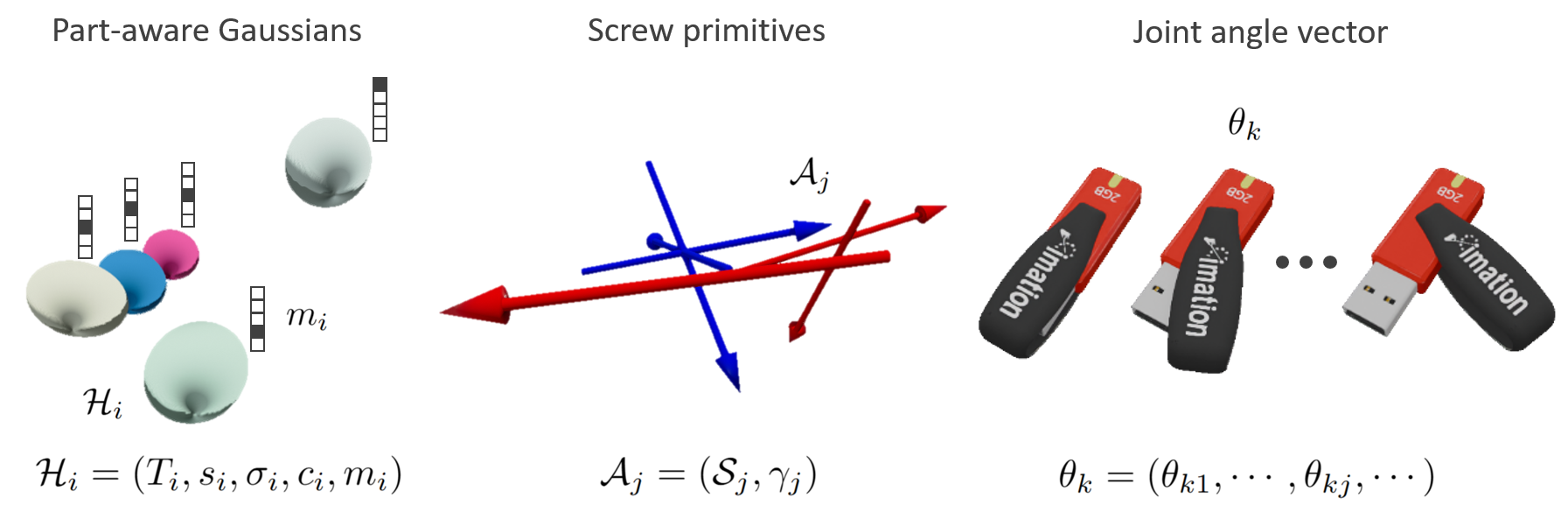
First, we splat screw primitives, where the \( j \)th screw primitive \( \mathcal{A}_j \) is parametrized by a tuple \( (\mathcal{S}_j, \gamma_j) \), with \( \mathcal{S}_j \) representing a screw axis and \( \gamma_j \in [0, 1] \) denoting the confidence.

Next, we splat part-aware Gaussian primitives, where the \( i \)th primitive \( \mathcal{H}_i \) is parametrized by an augmented tuple \( (T_i, s_i, \sigma_i, c_i, m_i) \). The paremeters \( (T_i, s_i, \sigma_i, c_i) \) are identical to those of Gaussians in standard Gaussian splatting. Here, \( m_i = (m_{i0}, \cdots, m_{ij}, \cdots) \) represents a probability simplex over the parts defined by screw primitives. Specifically, \( m_{i0} \) denotes the probability that the Gaussian belongs to the static base part, while \( m_{ij} \) for \( j \geq 1 \) denotes the probability that the Gaussian is associated with the part whose motion is governed by the \( j \)th screw primitive \( \mathcal{A}_j \).

Lastly, we assign a joint angle vector \( \theta_k = (\theta_{k1}, \cdots, \theta_{kj}, \cdots) \) to the RGB observations corresponding to the \( k \)th configuration of the articulated object. Specifically, \( \theta_{kj} \) denotes the joint angle associated with the \( j \)th screw primitive \( \mathcal{A}_j \) in the \( k \)th configuration.

The key idea behind the RGB rendering procedure is to replicate Gaussians from each part-aware Gaussian primitive and assign each replica to either the static base or one of the movable parts. Specifically, we construct Gaussians \( \mathcal{G}_{ij} \) from the \( i \) th part-aware Gaussian primitive \( \mathcal{H}_i \). Each Gaussian \(\mathcal{G}_{ij}\) is assigned to the base part if \( j = 0 \), and to the movable part associated with the screw primitive \( \mathcal{A}_j \) if \(j \geq 1\).

The part-aware Gaussian primitives, screw primitives, and joint angles are jointly optimized to minimize the following loss function: $$ \begin{equation*} \mathcal{L} = \mathcal{L}_{\text{render}} + \beta \sum_{j} \sqrt{\gamma_j}, \end{equation*} $$ where \( \mathcal{L}_{\text{render}} \) is the RGB rendering loss. The second term serves as a regularization term -- referred to as the parsimony loss -- which encourages ScrewSplat to represent articulated objects using the smallest possible number of screw primitives. This term not only pushes the model to select a minimal set of screws, but also promotes the identification of the most reliable ones.

The optimized ScrewSplat serves as an RGB image renderer conditioned on the joint angle vector \( \theta \); that is, the visual appearance (i.e., RGB image) of the articulated object \( I \) from an arbitrary camera pose can be obtained through a continuous -- and even differentiable -- function \( \pi \), such that \( I = \pi(\theta) \). Using this, we focus on controlling the joint angles of an articulated object to match a given text prompt using visual foundation models. Specifically, given the current visual appearance of the object and a text description of its current state, along with a target text prompt, our goal is to find a joint angle vector \( \theta \) such that the rendered appearance \( I = \pi(\theta) \) aligns with the target prompt.

We demonstrate the effectiveness of ScrewSplat in zero-shot, text-guided manipulation tasks, highlighting its practical utility in real-world robotic scenarios. Specifically, ScrewSplat accurately recognizes both the 3D geometry and kinematic structure of real-world objects — even in challenging cases such as a translucent drawer. A well-trained ScrewSplat further enables precise estimation of current joint angles and facilitates successful text-guided object manipulation.